Elphel Development Blog

GTX_GPL – Free Software Verilog module to simulate a proprietary FPGA primitive

Widespread high-speed protocols, which are based on serial interfaces, have become easier and easier to implement on FPGAs. If you take a look at Xilinx’s chips series, you can monitor an evolution of embedded transceivers from some awkwardly inflexible models to much more compatible ones. Nowadays even the affordable 7 series FPGAs possess GTX transceivers. Basically, they represent a unification of various protocols phy-levels, where the versatility is provided by parameters and control input signals.
The problem is, for some reason GTX’s simulation model is a secured IP block. It means that without proprietary software it’s impossible to compile and simulate the transceiver. Moreover, we use Icarus Verilog for these purposes, which doesn’t provide deciphering capabilities for now, and doesn’t seem to ever be able to do so: http://sourceforge.net/p/iverilog/feature-requests/35/

Still, our NC393 camera has to use GTX as a part of SATA host controller design. That’s why it was decided to create a small simulation model, which shall behave as GTX, at least within some limitation and assumption. This was done so that we could create a full-fledged non-synthesizable verification environment and provide our customers with a universal within simulation purposes solution.

The project itself can be found at github. The implementation is still crude and contains only the bare minimum required to achieve our goals. However, it assumes a possibility to be broadened onto another protocol’s case. That’s why it preserves the original GTX structure, as it’s presented in Xilinx’s “7 Series FPGAs GTX/GTH Transceivers User Guide v1.11”, also known as UG476: http://www.xilinx.com/support/documentation/user_guides/ug476_7Series_Transceivers.pdf
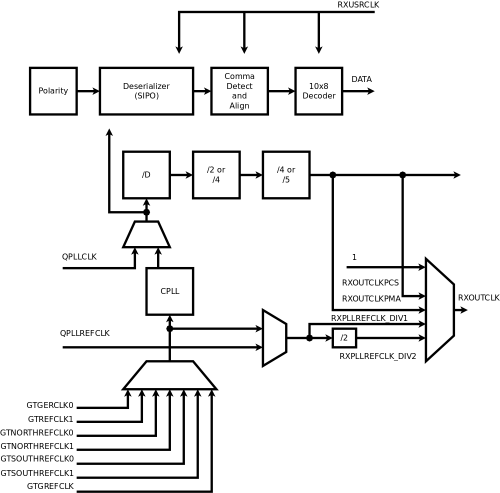
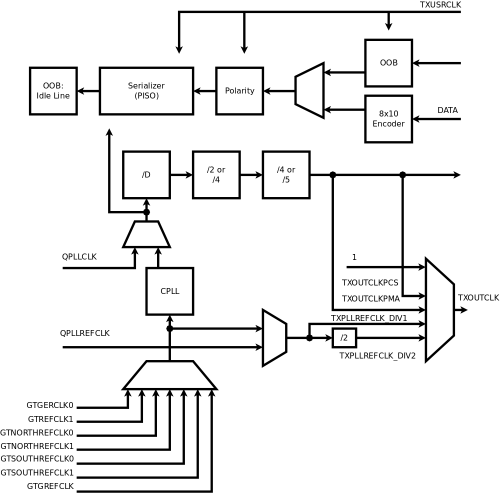
The overall design of the so called GTX_GPL is split into 4 parts, contained in a wrapper to ensure interface compatibility with the original GTX. These parts are: TX – transmitter, RX – receiver, channel clocking and common clocking.
All of the clocking scheme was based on an assumption of clocks, PLLs, and interconnects being ideal, so no setup/hold violation/metastability are expected. That itself makes the design non-synthesizable, but greatly reduces its complexity.

Transmitter and receiver schemes are presented in the figures. Each is provided with a clocking mechanism. You can compare it to GTX’s corresponding schemes (see UG476, pages 107, 133, 149, 169). As you can see, TX and RX lack the original functional blocks. However, many of them are important only for synthesis or precise post-synthesis simulation, like phase adjustments or analog-level blocks. Some of them (like the gearbox) are excessive for SATA and implementing them can be costly.
Despite all of that, current implementation passes some basic tests when SATA parameters are turned on. Resulting waves were compared to ones received by swapping GTX_GPL with the original GTX_CHANNEL primitive as a device-under-test, and they showed more or less the same behavior.

You can access to a current version via github. It’s not necessary to clone or download the whole repository, but enough to acquire ‘GTXE2_CHANNEL.v’ file from there. This file represents a collection of all necessary modules from the repository, with GTXE2_CHANNEL as a top. After including (or linking as a lib file/source file) it in your project, the original unisims primitive GTXE2_CHANNEL.v will be overridden.

If you find some bugs during simulation in SATA context or you want some features to be implemented (within any protocol’s set-up), feel free to leave a message via comments, PM or github.

Overall, the design shall be useful for verification purposes. It allows to create a proper GPL licensed simulation verification environment which is not hard-bound to a proprietary software.