FFT256
by Oleg Dzhimiev
1. [Done] Add headers and commit to CVS.
2. [Done] Optimize BRAM usage.
4 BRAMs & 8 MULTs, ~150MHz after Synthesis (will be less of course after implementation)
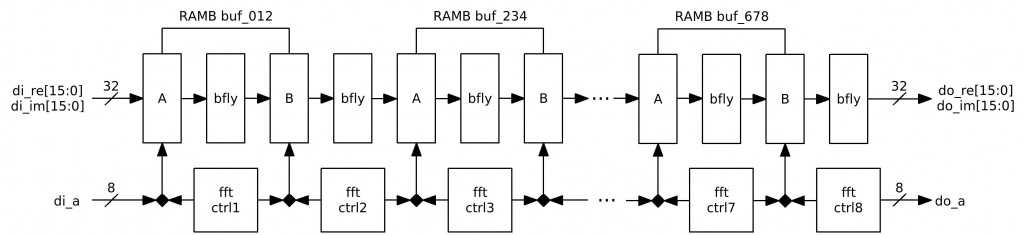
Fig.1 FFT256 diagram
3. [In Progress] FFT256 Verification.
NOTES:
- Do wires to BRAM36X36 and to MULT18X18 are shared? Can I use all 28 BRAMs and 28 MULTs in one design?
TODO:
- Check if the FFT256 results are correct.
- Write a correlation computation block.
- Write complex multiplication of 2 FFT256s (in order to get a cross-correlation spectrum)
- Add IFFT256 run for the multiplication result.
Oleg, couple notes.
1) 32 (36) bit wide BRAM port is not compatible with multiplier, you have to use 16(18) bit wide. That was once my big disappointment – a had to change all the memories from 32(36) to 16(18) bitS.
You know – Spartan 3e has combined BRAM/Mult cells, so you can use both devices, but _only_ if both ports of BRAM are less than 32. Otherwise – it will be either/or (MULT _or_ BRAM)
2) Multipliers support 18-bit operands (17+sign). Memory also support 18 bits. You do not need to have re/im data to be rounded/truncated to 16-bits.
I remember, Andrey, you were talking about this earlier – so I left a note.
If to use 16(18) then there will be a need:
A) to use twice more BRAM blocks (8) to be able to perform 8 256-pixel sequences at a time in conveyor.
Or
B) to make the fft two times slower.
@2592×1944:
A) 2ffts+1ifft will eat 24 MULTs + 24 BRAMs and will take 0.5s + time for 2ffts multiplication. 4 BRAMs are left for the memory controller and other logic.
B) 2ffts+1ifft – 24 MULTs + 12 BRAMs and ~ 1s + time for 2ffts multiplication
I’ll try to optimize it somehow (avoid B) ). Maybe instantiate buffers as arrays or use logic for some of them.
Oleg, Do you really need BRAMs between each pass? As I remember you reorder data only once – either before or after all 8 passes, so if the passes are pipelined – no need to full buffering, distributed RAM should do.
At least – each other pass? Take pairs of passes, see which next stage butterflies depend on which ones from the previous one, define the sequence in which butterflies are calculated so intermediate between-stages memory is small and fits into 16-cell distributed (always register after the distributed memory – by itself it is slower).
Other pipeline-optimized sequences that require less memory (so fit into distributed)?
Also – I remember you had 4 clock cycles per butterfly, BRAM is dual port (so read and write can be simultaneous – just matching internal latencies). Even if you read/write just 18-bit words (2 clocks per re/im pair) single BRAM can serve 2 FFT stages (4 clocks/2 clocks=2). Did I miss something?
BTW. http://www.cmlab.csie.ntu.edu.tw/cml/dsp/training/coding/transform/fft.html (TC.3.1 Number of Nontrivial Real Multiplcations and Additions to Compute an N-point Complex DFT) shows that for 256 points you need just 1800 non-trivial real multiplications and 5896 additions. You can not really remove _all_ trivial multiplications, but you can easily do it for the first 2 (or last 2 depending on the implementation) FFT stages – no multipliers there.
When selecting between shuffle before/after – try to make the algorithm such that you can extract FFTs for smaller lengths (i.e. 16 or 32) as intermediate results (so we can increase resolution later)
Andrey, you are right – full buffering can be avoided – each N-th stage needs 2+2^(N-1) size buffer.
Here’s an example for 16 points with pre reverted bits and keeping addresses:
stage1: (00,08)(04,12)(02,10)(06,14)…
stage2: (00,04)(08,12)(02,06)(10,14)…
stage3: (00,02)(04,06)(08,10)(12,14)…
I’ll make a clearer explanation, maybe with a picture.
And my version is with full buffering – I’ve just tried to use distributed RAMs – and it ate 106% of SLICEMs
Oleg, yes, something like this.
And – again I would advise to use extra registers to get the top clock rate – use registers between stages even when those stages have embedded registers (like multipliers or memories), because those registers have different timing. Additionally extra (distributed) registers provide more flexibility during P&R so you’ll get higher clock rate. It would be larger job to add extra register layers later (as I had to do many times) and re-adjust the latencies.
Yes, I use registers – before/after multiplication, sum, BRAM.
“extract FFTs for smaller lengths”
This is a problem. Because if to use the popular methods DIF or DIT then for FFT256 it’s not a trivial thing to get a sub-FFT128 for 0-127 points and a one for 128-255, easy only for sequences of even and odd points – as each FFT stage performed backwards is a decomposition on smaller FFT_odd & FFT_even (at least in the Decimation-In-Time algorithm).
I still think it is possible to do something to combine 16 of 16-point FFT results to make a 256 one. And as we need consecutive points in time it will be decimation in frequency